實作RSA + AES 的檔案加密算法POC
為了做到檔案的加密(後來才知道其實用GPG就可以了)
一開始我只是想說用現成套件不同的 金鑰key值作為參數,結合ChatGpt就開始做POC看看了
大不了是換演算法的問題,結果其實數位簽章 除了格式、作業系統管理的模式、公私鑰檔案其實也有不同的規定
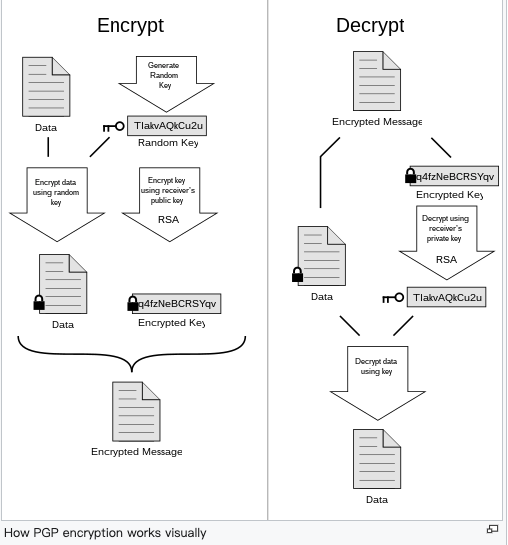
但大至上心得是一開始想說讓 檔案加密,而且是透過Public Key進行,然後對方用 Private Key解密,所以我出發點就是用RSA演算法去進行加密,結果發現怎麼都會發生長度錯誤的問題。
後來深究後才發現RSA的加密無法對長度太大的東西進行,所以後來換成短字串果然就可以了
因此思考了加解密該做的事情後,就做了一個AES + RSA的POC,RSA主要用來加密 AES的Key
後來果然發現這個跟GPG的作法有點像~~
實作POC如下∶
using System.Security.Cryptography;
string keyBase64 = string.Empty;
using (Aes aesAlgorithm = Aes.Create())
{
aesAlgorithm.KeySize = 256;
aesAlgorithm.GenerateKey();
keyBase64 = Convert.ToBase64String(aesAlgorithm.Key);
Console.WriteLine($”Aes Key Size : {aesAlgorithm.KeySize}”);
Console.WriteLine(“Here is the Aes key in Base64:”);
Console.WriteLine(keyBase64);
Console.ReadKey();
}
string filePath = “/Users/paul_huang/Desktop/FileEncryptTest”;
GenerateKeys(filePath);
// 設定公鑰和私鑰檔案路徑
string publicKeyPath = Path.Combine(filePath, “publicKey.pem”);
string privateKeyPath = Path.Combine(filePath, “privateKey.pem”);
// 設定金鑰的位元數
var keyString = keyBase64;
// 檢查檔案是否存在
if (!File.Exists(publicKeyPath) || !File.Exists(privateKeyPath))
{
Console.WriteLine(“找不到金鑰檔案。請確保金鑰檔案存在。”);
return;
}
// 讀取公鑰
string publicKey = File.ReadAllText(publicKeyPath);
// 讀取私鑰
string privateKey = File.ReadAllText(privateKeyPath);
// 設定要加密的檔案路徑
// 加密檔案
var keyFileName = “key.txt”;
var keyFilePath = Path.Combine(filePath, keyFileName );
if (File.Exists(keyFilePath) == false)
{
File.WriteAllText(keyFilePath, keyString);
}
else
{
keyString = File.ReadAllText(keyFilePath);
}
EncryptKeyFile(keyFilePath, publicKey);
DecryptKeyFile($”{keyFilePath}.encrypted”, privateKey);
// var encryptedKey = $”{keyFilePath}.encrypted”;
var encryptFile = “paul.jpg”;
var encryptFilePath = Path.Combine(filePath, encryptFile);
var encryptedFileContentString = Encrypt(Convert.ToBase64String(File.ReadAllBytes(encryptFilePath)), keyString);
File.WriteAllText(encryptFilePath+”.encrypted”, encryptedFileContentString);
File.WriteAllBytes(encryptFilePath + “decrypted”, Convert.FromBase64String(Decrypt(encryptedFileContentString, keyString)));
static void EncryptKeyFile(string filePath, string publicKey)
{
try
{
byte[] dataToEncrypt = File.ReadAllBytes(filePath);
using var rsa = new RSACryptoServiceProvider(2048);
rsa.FromXmlString(publicKey);
byte[] encryptedData = rsa.Encrypt(dataToEncrypt, false);
// 寫入加密後的檔案
File.WriteAllBytes($”{filePath}.encrypted”, encryptedData);
Console.WriteLine(“檔案已成功加密。”);
}
catch (Exception ex)
{
Console.WriteLine($”加密時發生錯誤: {ex.Message}”);
}
}
static void DecryptKeyFile(string encryptedFilePath, string privateKey)
{
try
{
byte[] encryptedData = File.ReadAllBytes(encryptedFilePath);
using (RSACryptoServiceProvider rsa = new RSACryptoServiceProvider(2048))
{
rsa.FromXmlString(privateKey);
byte[] decryptedData = rsa.Decrypt(encryptedData, false);
// 寫入解密後的檔案
File.WriteAllBytes($”{encryptedFilePath}.decrypted”, decryptedData);
Console.WriteLine(“檔案已成功解密。”);
}
}
catch (Exception ex)
{
Console.WriteLine($”解密時發生錯誤: {ex.Message}”);
}
}
static string Encrypt(string plainText, string key)
{
using (Aes aesAlg = Aes.Create())
{
aesAlg.KeySize = 256; // Set key size to 256 bits
aesAlg.Key = Convert.FromBase64String(key);
aesAlg.IV = new byte[16]; // AES uses a 128-bit IV
ICryptoTransform encryptor = aesAlg.CreateEncryptor(aesAlg.Key, aesAlg.IV);
using (MemoryStream msEncrypt = new MemoryStream())
{
using (CryptoStream csEncrypt = new CryptoStream(msEncrypt, encryptor, CryptoStreamMode.Write))
{
using (StreamWriter swEncrypt = new StreamWriter(csEncrypt))
{
swEncrypt.Write(plainText);
}
}
return Convert.ToBase64String(msEncrypt.ToArray());
}
}
}
static string Decrypt(string cipherText, string key)
{
using (Aes aesAlg = Aes.Create())
{
aesAlg.KeySize = 256; // Set key size to 256 bits
aesAlg.Key = Convert.FromBase64String(key);
aesAlg.IV = new byte[16];
ICryptoTransform decryptor = aesAlg.CreateDecryptor(aesAlg.Key, aesAlg.IV);
using (MemoryStream msDecrypt = new MemoryStream(Convert.FromBase64String(cipherText)))
{
using (CryptoStream csDecrypt = new CryptoStream(msDecrypt, decryptor, CryptoStreamMode.Read))
{
using (StreamReader srDecrypt = new StreamReader(csDecrypt))
{
return srDecrypt.ReadToEnd();
}
}
}
}
}
static void GenerateKeys(string path)
{
try
{
using (RSACryptoServiceProvider rsa = new RSACryptoServiceProvider(2048))
{
// 公鑰
string publicKey = rsa.ToXmlString(false);
Console.WriteLine(“公鑰:”);
Console.WriteLine(publicKey);
// 私鑰
string privateKey = rsa.ToXmlString(true);
Console.WriteLine(“\n私鑰:”);
Console.WriteLine(privateKey);
// 將金鑰寫入檔案
File.WriteAllText(Path.Combine(path, “publicKey.pem”), publicKey);
File.WriteAllText(Path.Combine(path, “privateKey.pem”), privateKey);
Console.WriteLine(“\n金鑰已成功生成並保存至檔案。”);
}
}
catch (Exception ex)
{
Console.WriteLine($”生成金鑰時發生錯誤: {ex.Message}”);
}
}
static string GenerateRandomKey(int length)
{
// 使用 RNGCryptoServiceProvider 產生安全的亂數
using (var rng = new RNGCryptoServiceProvider())
{
// 建立位元組陣列來存放隨機資料
byte[] randomBytes = new byte[length];
// 將亂數填入位元組陣列
rng.GetBytes(randomBytes);
// 將位元組轉換成十六進位字串
string randomKey = BitConverter.ToString(randomBytes).Replace(“-“, “”);
return randomKey;
}
}